Classical Western Music is based on a discrete set of frequencies with clearly defined pitches: the musical notes. Musical systems as different as tonality, modality or serialism constitute ultimately alternative ways to organize tones and semitones. Although, among Western composers, there are also some trials of using smaller frequency steps (as the microtonality of Alois Hába), the essential discrete nature of the explored frequency space is in any case preserved. In fact, our 5-line based musical notation evolved under this premise -the existence of musical notes-, and worked perfectly to transmit the essential musical content of these styles. But, what happens when we try to apply our system of musical notation to other musical traditions? Let's begin with the quote of a sharp paragraph by Nicholas Cook:

Some ethnomusicologists are prepared to use staff notation to transcribe the music they study, as a means both of understanding it and of communicating that understanding to their readers. But they are painfully conscious that in doing this they are shoehorning Indian or Chinese music, or whatever it might be, into a system that was never designed for it. [In florid singing] trying to say where one note starts and another stops, as 'note' would be defined in terms of staff notation, becomes a completely arbitrary exercise; the music just doesn't work that way. There is a collision between music and notation.^[1]

This very same collision applies to many chants of the Spanish Flamenco music. In a work with the musicologist Teresa Ruiz Coll, we studied the problem of notation of vocal microtonality and look for ways to overcome the conflict.^[2]

Let me illustrate the problem (and its potential ways of solution) with audible examples. Our reference sound corresponds to the record of a melismatic (ornamental) section of the chant Mis caramelos (My candies)^[3]:

What appears in any traditional 5-line musical score are the fundamentals of the sounds to be listened. A timbre -the set of harmonics that provide the sound with it's color- is added when the score is played by a particular instrument. So, we are essentially interested in the sucessive values of the fundamental (or first harmonic) of the chant. A plot with the time evolution of the frequency of such fundamental is known as a melogram, being its values extracted from a given sound by using pitch detection algorithms, PDA^[4]. The following melogram corresponds to our chant excerpt.

We can synthesize a sinusoidal wave whose frequency evolves following the melogram curve. The resulting sound is a precise version of the chant in which the color of the singer voice of has been completely removed, this is, a chant with no timbre:

The fundamental moves in the frequency space in a continuous way. To produce a traditional score we have to approach this curve by discrete horizontal segments. We made this process by applying discretization algorithms that we adapted from those used in biological sciences to discretize continuous microarray data^[5]. The following plot shows the result of applying such methods to the melogram.

Next, each segment has to be rounded to the closest semitone to produce a tempered score (in tuned tones and semitones).

And this is the resulting transcription in conventional music notation, a score that can also be performed by the same type of sinusoidal wave used before:

Although this sound still keeps some recognizable features of the chant (compare with the first sinusoidal sound), there are so many missing details that the essence of what we understand by a Flamenco melody is almost totally lost. Could this be caused by the fact that a semitonal scale is a too raw approach? What if we tried a transcription using smaller frequency chunks (as in the microtonality of Alois Hába)? In the following plot the discretization (in cyan) has been approached to the closest quarter-tone (in red).

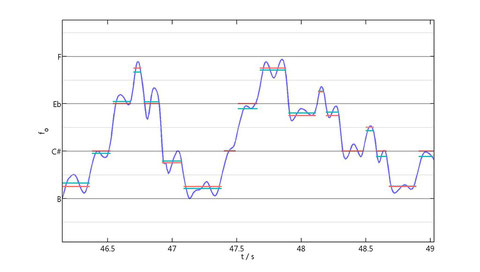
The adjusted segments (in red) were subsequentely converted to a microtonal score and sound:

Paradoxically, although we are now closer to the original chant, the quarter-tone approach introduces an out-of-tune effect that was not perceived in that chant. Ultimately, a smooth movement between frequencies seems to be an essential component of these styles, a movement that is lost in the discrete simplifications. In consequence, we looked for alternative ways to encode the essence of these chants with the minimal amount of information -indeed, what a music score does. This time, instead of averaging segments of frequency, we focused on the values of the local extremes in the melogram (the cyan dots in the following figure).

Note that, since the melogram curve is so smooth, we can encode it almost perfectly by keeping only the values of the local extremes:

We can reconstruct it by interpolating the rest of values with cubic splines –a mathematical function that is used to fit a series of points in a smooth way.

You can check how close the result of the spline-based reconstruction is from the original sinusoidal sound:

Now, we can take advantage of this procedure to produce an alternative score. In this case, what we are going to approach to a discrete set of frequencies are just the extremes. We first approach the extremes to the closest note and then fit the new extremes with the splines. In the following plot, extremes have been successively approached to the closest semitone, quarter-tone and octave-tone respectively.

You can compare the respective resulting sounds: the semitone reconstruction,

the quarter-tone one,

and the octave-tone one,

The smaller the frequency chunks, the closer the sound to the original one. However, the translation into musical notation becomes more and more unfriendly as smaller intervals are considered. The following score corresponds to the quarter-tone adjustment. The spline is translated into musical notation as a glissando sign.

In any case, I personally think that the simpler semitonal spline is able to conserve most of the ethnic flavor the original chant -much more than the segmentation-based semitonal transcription above.

In summary, when dealing with the transcription of melodies belonging to styles -as the Spanish Flamenco or the Hindustani and Carnatic classical styles from India- in which a continuous space of frequencies is exhaustively explored, there is a trade-off between accuracy and readability. If the performer is a machine, the first melogram could be used directly as a music score. For example, by applying its frequency values to the MIDI pitch bend,

or by assigning them to a FM synthetic sound:

Aside of the ability of the player, the goal of the transcription (musicology, performance, and so on) should be also considered to select among the alternative solutions above. The fact that we can still identify the original chant from the first semitonal score that we produced, implies that not every frequency in the melogram has the same importance for the melody structure. In other words, there are scalistic (although blurred) references for these chants. Indeed, that score corresponded to the Phrygian mode that characterizes most Spanish traditional music.

1. Nicholas Cook, Music: A very short introduction. Oxford University Press (Oxford, 1998), p. 59.

2. Ruiz-Coll, Teresa and Camas, Francisco M., Notation of continuous vocal pitches in etnomusicology (Under revision).

3. Mis caramelos or Pregón de Macandé is the cry of a street vendor that promotes his candies. It was created by the street vendor Macandé (Cádiz, 1897-1947). This performance by José de los Reyes Santos (from El Puerto de Santa María) is included in the Magna Antología del Cante Flamenco (Hispavox, 1971), an exhaustive compilation of Flamenco chants.

4. We used the PDA explained in Sun, X., Pitch determination and voice quality analysis using subharmonic-to-harmonic ratio. Orlando (Florida): Proc. of ICASSP2002 (May, 2002).

5. See, for example, Picard, Frank et al. A statistical approach for array CGH data analysis. BMC Bioinformatics (2005) vol. 6, 27.